¿Quién dijo que las matemáticas no eran divertidas? Este verano se activan las neuronas y se desafía el coeficiente junto al profesor Mauricio Ramseyer.
Valeria Elías
RTS Medios
La geometría se suma al verano, junto a la matemáticas presenta un desafío que el profesor Mauricio Ramseyer trae el día de hoy.
Círculos en cajas
La situación es la siguiente, se tiene una caja rectangular de lado 60cm, donde se tiene que guardar un círculo cuyo radio (recordar que es la distancia que hay desde el centro del círculo a cualquiera de los puntos del borde) no se conoce y le vamos a llamar R. Queremos construir la caja de manera el otro lado mida R + 15, y entonces colocar el círculo dentro. La pregunta, en principio, es ¿cuál es radio máximo que podemos hacer para que el círculo entre en la caja? Si esto parece sencillo, cambiemos la pregunta. Supongamos que la caja tiene una separación en la diagonal del rectángulo. ¿Te animarías a responder la misma pregunta? Es decir, con el agregado de la diagonal, uno podría pensar en un triángulo rectángulo y preguntarse por el radio máximo que debe tener el círculo para entrar. Bien, ese es el desafío. A veces, en matemática, un simple cambio como agregar una diagonal, puede significar que el problema sea más interesante de pensar.
Solución al problema
Si no hay diagonal entonces como el otro lado debe medir 15 unidades más el radio de la pelotita, si la pelotita es pequeña, entonces sobra mucho espacio, si la pelotita tiene un radio muy grande, entonces ya no entra (ver los dibujitos para convencerse)
Por lo tanto, el radio máximo que podemos considerar es una bolita de radio 15 puesto que más grande queda afuera y más pequeña sobra espacio.
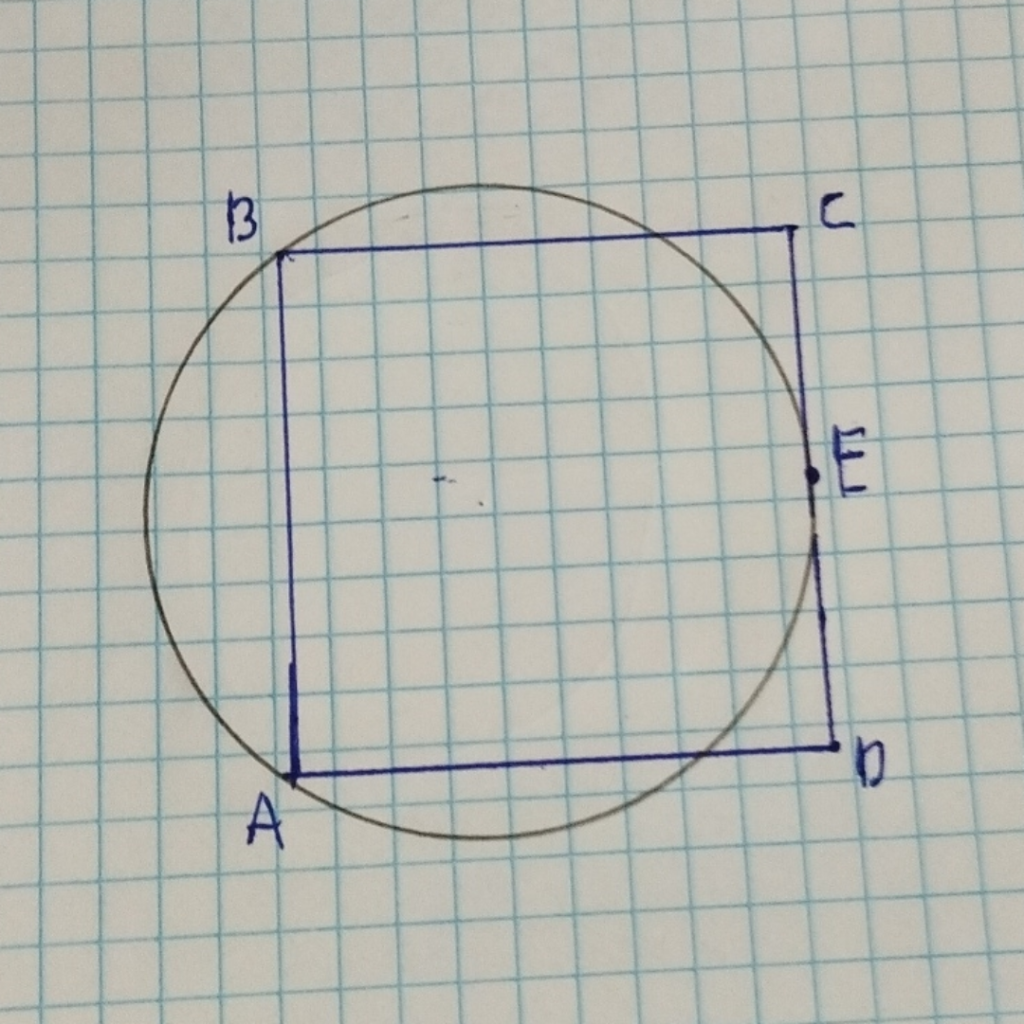
Cuando tenemos una diagonal en el medio la cosa cambia
Podemos simplificar el problema a un triángulo y trabajar ahí. La pelotita más grande que podemos poner si la diagonal nos frena es una pelotita de radio 10 y aquí hay que valerse de la famosa relación pitagórica que afirma que “en todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa”.
¿Coincide tu respuesta? Como ves, la clave para resolver estos acertijos no suele ser hacer cálculos complejos, sino pensar con orden, plantearse el peor escenario posible o atreverse a cambiar la perspectiva. La lógica es una herramienta poderosa y divertida.
Fuente: RTS Noticias
